Here's a brief description of the experiment:
First, I reviewed each team's rating history and from that, using statistical tools, assigned each team a rating. In the experiment, each team's assigned rating and rank is its actual strength. Each team always performs at this actual strength level.
Second, I took last year's regular season schedule and determined the outcome of every game, based on the teams' actual strength and the value of home field advantage. Based on in-conference results, I also set up conference tournaments including their outcomes based on the teams' actual strength and the value of home field advantage.
Third, with all those game results as the data base, I applied the NCAA's ARPI formula to see what ratings and ranks the formula would give to teams.
So, you'd expect that teams' ranks at the end of the process using the NCAA's ARPI formula would be about the same as the actual strength ranks I assigned them and that determined the outcomes of all games, right?
Not exactly. In fact, in many cases teams' ranks according to the NCAA's ARPI formula are not close to their actual strength ranks. And this includes a significant number of cases in which it would matter for NCAA Tournament at large selection purposes.
Here's a table that demonstrates that, with an explanation below the table:
In the table, the Simulated 2019 Rank column is the actual strength ranks I assigned, for the top 125 the teams. In the experiment, these are the ranks that determined the outcomes of all games. The 2019 ARPI Rank column is the ranks the NCAA's ARPI formula gave the teams after applying the formula to the game results that the actual strength ranks produced. In each rank column, I've color coded the top 60 teams. In the column with the team names, I've color coded blue the teams that are within the actual ranks top 60 but outside the ARPI formula's top 60. I've color coded grey the teams that are outside the actual ranks top 60 but within the ARPI formula's top 60. I've focused on the top 60 because, for practical purposes the ARPI formula's top 60 are the teams the Women's Soccer Committee considers as potential candidates for at large selections. (In fact, no team ranked poorer than #57 has gotten an at large selection over the last 12 years.)
As you can see, there are 13 teams whose actual strength puts them in the top 60, but that are outside the ARPI formula's top 60. And conversely, there are 13 teams whose actual strength puts them outside the top 60, but that are inside the ARPI formula's top 60.
So, why are there differences between teams' actual strength ranks and the ranks the ARPI formula gives them? The differences are due to one, and only one, thing: the interaction between the NCAA's RPI formula and the teams' schedules.
I'm going to use Clemson's and Hofstra's results, in my experiment, to show this.
CLEMSON
In the experiment, Clemson's actual strength rank is #20, and all its results are consistent with that rank. Yet the NCAA's RPI formula, when applied to those results, comes up with a rank of #74. How can that be?
It is because of the way the NCAA's RPI measures strength of schedule. An opponent contributes to Clemson's strength of schedule based on the opponent's own winning percentage (against all the teams it played other than Clemson) and on its opponents' opponents' winning percentages. Under the RPI formula the effective weights of these two elements are roughly 80% the opponent's own winning percentage and 20% the opponents' opponents' winning percentages. In other words, the opponent's winning percentage is by far the strongest factor in the strength of schedule part of the RPI formula. Since most of what a team contributes to your strength of schedule is its winning percentage, this means that if you are looking at two teams with similar rankings, where one of them will fill a possible opponent slot in your schedule, you will be better off from an RPI formula perspective playing the team that will have the better winning percentage.
Here is a table for the in-conference ACC opponents Clemson played in my experiment (the ones it actually played in 2018):
In this table, teams' Actual Ranks are the actual strength ranks I assigned them, which determined the results of all games. The ARPI Ranks are the teams' ranks as determined by the NCAA's ARPI formula, applied to those game results. As you can see, in some cases the ARPI formula has seriously mis-ranked teams. The ARPI SoS Rank is the ARPI formula's rank of each opponent as a contributor to its opponents' strengths of schedule. As you can see, here again the ARPI formula has seriously mis-ranked teams. The Actual Rank to SoS Rank Difference is the difference between a team's actual strength rank and the rank the ARPI formula has assigned it as a contributor to its opponents' strengths of schedule.
At the bottom of the table are averages. Looking at that row, the average actual rank of Clemson's in-conference ACC opponents was 61. On the other hand, the ARPI formula only gave them an average rank of 73, meaning it under-ranked them by an average of 12 positions. And, as contributors to Clemson's strength of schedule, the ARPI formula only gave them an average rank of 115, meaning it under-ranked them by an average of 54 positions.
There's nothing Clemson can do about who its in-conference ACC opponents are. It's simply a fact of Clemson's life that the ARPI under-ranks them and that it under-ranks them even more as contributors to Clemson's strength of schedule.
So what does the table look like for Clemson's non-conference opponents? Here it is:
As you can see, the average actual strength rank of Clemson's non-conference opponents is 122. But the ARPI formula calculates their average rank as only 153, 31 positions poorer. And, their average contribution to Clemson's strength of schedule is only 184, 62 positions poorer.
When you put together the ARPI formula's under-ranking of Clemson's in-conference ACC opponents as strength of schedule contributors with the formula's similar under-ranking of Clemson's non-conference opponents, you get Clemson, with an actual strength rank of #20, receiving an ARPI formula rank of #74. At #20, Clemson would be a sure thing for an at large selection for the NCAA Tournament. At #74, it's out of the running.
So, could Clemson balance out its in-conference problem with better non-conference scheduling? Yes. Here's an alternative non-conference schedule that is equal in actual strength:
Where does this alternative schedule put Clemson? At #23 in the ARPI formula's rankings, 51 positions better than the actual schedule put it and right about where it should be given its actual strength rank of 20. And this is notwithstanding that the actual schedule and the alternative schedule have opponents essentially equal in actual strength. Simply put, smart scheduling in relation to the RPI formula has balanced out the problem Clemson has due to its ACC opponents' contributions to its strength of schedule being understated.
What's more, the Women's Soccer Committee if looking at the alternative schedule will think that Clemson has played non-conference opponents with an average rank of 99, since that is their average rank under the RPI formula. This is as compared to an average rank of 153 that the Committee will be seeing if looking at the actual schedule.
In other words, if you're Clemson in this experiment, smart scheduling in relation to the RPI formula is essential to realizing your NCAA Tournament aspirations. With Clemson's actual 2018 schedule, it's not in the Tournament. With an RPI-smart schedule, it's in.
But, there's one more bonus from Clemson's alternative "smart" schedule. Here's what its in-conference ACC table will look like when paired with that schedule:
This table shows that if Clemson plays the alternative "smart" schedule, its in-conference ACC opponents' average ARPI rank is 71. This is 2 positions better than if Clemson plays the actual schedule. In shifting schedules, Clemson hasn't changed its own winning percentage, but it has played opponents with better winning percentages. This, in turn, gets passed on to Clemson's ACC opponents through Clemson's contribution to their strengths of schedule.
Thus Clemson's smart scheduling can give it a large ARPI benefit and, at the same time, also can give a small benefit to its ACC opponents.
HOFSTRA
With Hofstra, for illustration, I'm going to show how poor scheduling can take a team from a good rank to a poor one.
In the experiment, Hofstra's actual strength rank is 70. But, with its actual schedule, the ARPI formula gives it a rank of 28. Let's look at its tables to see how this happened.
Here's its in-conference Colonial actual schedule:
You can see from this table that the ARPI formula, on average, under-ranks Colonial teams as contributors to their opponents' strengths of schedule, by 23 positions. This is similar to what the formula does to ACC teams except that for the ACC the problem is much more severe.
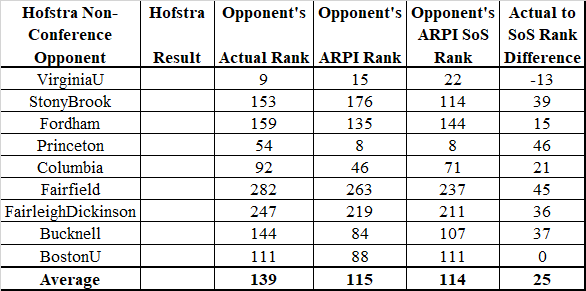
Here's Hofstra's actual non-conference schedule:
What you can see here is that (1) the RPI formula gives Hofstra's non-conference opponents significantly better ranks than their actual strength ranks and (2) the RPI formula likewise gives the non-conference opponents significantly better ranks as strength of schedule contributors. The result of this is that Hofstra, with an actual strength rank of 70 gets an RPI formula rank of 28. (This isn't just due to Hofstra's non-conference scheduling. Its smart scheduling is moving it up in the rankings, and other teams' not-smart scheduling is moving them down in the rankings. The cumulative effect of this is Hofstra ending up at #28.)
Suppose Hofstra had scheduled differently. Here's an alternative non-conference schedule of equal actual strength but producing competely different ARPI formula results:
With this non-conference schedule, Hofstra drops from the ARPI formula's rank of 28 to the formula's rank of 63. Yet this alternative schedule is equal in actual strength to Hofstra's actual schedule. It's just that these teams, due to the structure of the RPI formula, result in the formula grossly under-stating Hofstra's strength of schedule.
SUMMARY
If you're a team with NCAA Tournament aspirations, it's critical to schedule non-conference opponents with a view to how the RPI formula will see them as strength of schedule contributors. Especially if you're in a strong conference where it's hard to have a really good winning percentage, you're going to need all the boost to your strength of schedule that you can get. And, teams roughly equal in actual strength and in RPI rank often are not equal in strength of schedule contributor rank. So in selecting opponents, it's critical to pick ones not only who meet your objectives in terms of their actual strength and RPI rank, but also who will make good contributions to your RPI strength of schedule.
If you want a good tool for evaluating potential opponents with a view to their histories of actual strength, ARPI ranks, and ranks as contributors to opponents' strengths of schedule, there's a tool I created that's available at the RPI for Division I Women's Soccer website. It's in the form of a downloadable Excel workbook (free) and is an attachment at the bottom of the NCAA Tournament: Scheduling Towards the Tournament page. It has a page for each team from which you can get a picture of whether the team would be a good one for you to play given your schedule objectives. And it has summary pages that can be helpful. And, on its first page, it has a User Manual.
Remember, scheduling with a view to how the RPI formula will interact with your schedule matters. A lot.







No comments:
Post a Comment