NCAA TOURNAMENT: LIKELY AT LARGE CANDIDATE POOL AND SELECTION CHANGES IF THE COMMITTEE HAD USED THE BALANCED RPI RATHER THAN THE NCAA RPI

This article is on the question: Would it make a difference in NCAA Tournament at large selections if the Women's Soccer Committee used the Balanced RPI rather than the NCAA RPI?

The period covered is 2007 through 2023 (excluding Covid-affected 2020).  To determine what the at large selections would have been if the Committee had used the Balanced RPI, I took two steps:

1.  I assumed that under the Balanced RPI all at large selections would come from the Balanced RPI Top 57 teams.  I assumed this because since 2007, all at large selections have come from the NCAA RPI Top 57 teams (based on the current NCAA RPI formula).  From a practical perspective, there is no reason to think this would be different if the Committee were using the Balanced RPI: Everything would look similar to the Committee, it simply would looking at different rating numbers.

2.  One of the factors I use in evaluating Committee decisions is teams' good results (wins or ties) against Top 50 opponents.  I score these results using a system that is very heavily weighted towards good results against very highly ranked opponents.  Then I rank teams based on these scores.  Once I have these ranks, I combine them with their RPI ranks, with each rank weighted at 50%.  I then rank teams using their combined rank scores.  When I do that, the ranks on average match the Committee at large selections for all but 2 selections per year.  With that in mind, to see what the at large selections likely would have been if the Committee were using the Balanced RPI, I determine what their Top 50 results scores would have been using the Balanced RPI, rank teams accordingly, see what their combined Balanced RPI and Top 50 results score ranks would be with each weighted 50%, and rank them accordingly just as I do for the NCAA RPI and Top 50 results ranks.  I then assume that if the Committee were using the Balanced RPI, it would select teams based on their combined Balanced RPI and Top 50 results rank.

Looking at the numbers from 2007 through 2023, a change to the Balanced RPI would result, on average, in 6.3 new teams in the Top 57 per year -- in other words about 6 new teams per year would become candidates for at large selections and a matching 6 using the NCAA RPI would not be candidates.  Further, and more important, 3.6 different teams per year would get at large selections -- in other words 3 to 4 teams per year that did not get at large selections under the NCAA RPI would get them under the Balanced RPI and 3 to 4 teams that did get at large selections under the NCAA RPI would not get them.  Thus the answer to the question at the opening of this article is

Yes, it would make a difference in NCAA Tournament at large selections if the Women's Soccer Committee used the Balanced RPI rather than the NCAA RPI, to the tune of 3 to 4 different teams per year getting at large selections, on average.

When looking at conferences, here are the results of a rating system change for the 2007 through 2023 period:

In the table, the Net At Large Gain or Loss column shows the difference between the Committee's actual at large selections using the NCAA RPI and what the selections likely would have been if the Committee had used the Balanced RPI.

As you can see, the conference hurt the most by the NCAA RPI is the Big 10, which lost 16 at large positions from 2007 through 2023 due to use of the NCAA RPI, or 1 position per year on average.  Of the five conferences hurt by the NCAA RPI, three are from the West:  the Pac12, West Coast, and Big West conferences.  The other conference hurt is the ACC.

The conferences that benefit the most from the NCAA RPI are the Big East, SEC, Colonial, American, Atlantic Ten, and Big 12, with a number of other conferences helped just once over the 16-year period.

In the table, the Net Top 57 Gain or Loss column shows the difference in the number of teams a conference had in the Top 57 candidate pools for at large selections.  Note that 4 of the 6 conferences hurt by the NCAA RPI are from the West.

When looking a geographic regions, here are the results of a rating system change:

NOTE:  There are two sets of "new" at large selections under the Balanced RPI.  One set is teams that were outside the NCAA RPI Top 57 that, on coming into the Top 57 under the Balanced RPI, get at large selections.  The second set is teams that were inside the NCAA RPI Top 57 and did not get at large selections, but that under the Balanced RPI would get at large selections.  In the table, the Middle region is an example of having some from each set.

In the next post, I will pull together key information from this and other recent posts to show how all the information inter-relates.

A LOOK AT THE COMMITTEE'S NCAA TOURNAMENT BRACKET DECISIONS BATTING AVERAGE, 2011 - 2023

This is a review of how teams from the different regions and conferences do in NCAA Tournaments, as compared to how the Women's Soccer Committee expects them to do as indicated by its bracketing decisions.  The review covers the period from 2011 to 2023.  It starts at 2011 because in 2010 and earlier, seeded teams were not guaranteed to host first round games.

The review method assumes that for any pairing of teams:

1.  In a game between a seeded team and an unseeded team, the Committee expects the seeded team to win;

2.  In a game between two seeded teams, the Committee expects the better seeded team to win; 

3.  In a game between unseeded teams where the Committee awards one of them home field, the Committee expects the home team to win; and

4.  In a game between unseeded teams at a neutral site, the Committee has no expectation as to which team will win.

The review looks at the data through three lenses:

1.  Actual Games Played.  It looks at games teams actually played:

a.  For each game, it compares the Committee's expected result to the actual result.

 b.  For each team, for the games it played, it then tallies its expected wins and its actual wins.

c.  For each team, it then subtracts its expected wins from its actual wins.  If the result is a + number, it means the team won that many more of its games than the Committee expected.  If the result is a - number, it means the team won that many fewer.

d.  It then sums up the results from Step c by region and by conference, to see what the regions' and conferences' net results in actual games have been as compared to the Committee's expectations.

e.  It then expresses the results from Step d as a percentage of all games the region's or conference's teams played. 

2.  Expected Games.  It looks at how the Committee initially expected the bracket to play out:

a.  For each team, it looks at the number of games the Committee expected the team to win over the course of the Tournament.  For example, the Committee expects the overall #1 team (top left of the bracket) to win the championship, which means winning 6 games.  It expects the overall #2 team (bottom right) to win 5 games.

b,  For each team, it tallies the number of games it actually won.

c.  For each team, it then subtracts its expected wins from its actual wins.

d.  It then sums up the results from Step c by region and by conference, to see what the regions' and conferences' actual results have been as compared to the results the Committee expected them to have over the course of the Tournament.

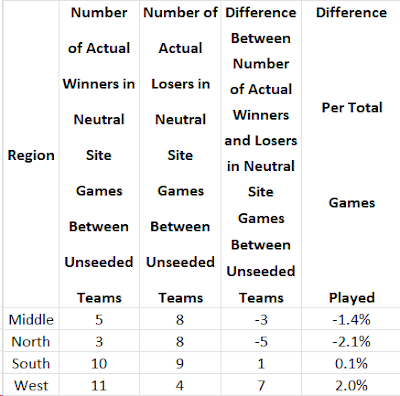
3.  Unseeded Opponents at Neutral Sites.  Method 1 leaves out one set of games: those between unseeded opponents at neutral sites.  In each of these games, at least one of the opponents has upset its opponent in a preceding round.  Since neither team is seeded and the game is at a neutral site, it is not possible to say that the Committee expected one or the other team to win.  On average, there are 2 to 3 games per year in this category. For these games:

a. For each region and conference, it sums up the number of games its teams won and the number they lost.

b.  For each region and conference, it then subtracts its number of games lost from its number of games won.  A + result means the region or conference won that many more than it lost and a - result means it lost that many more than it won.

c.   It then expresses the results from Step b as a percentage of all games the region's or conference's teams played.

Here are the results of the review, first by regions and then by conferences:

Regions

Teams' regions are based on the states where they are located.  The states are assigned to the regions in which the states' teams play the majority (or plurality) of their games.

Actual Games Played Method

Using the Middle region as an example, from 2011 through 2023, the net difference between the games it actually won and the games the Committee expected it to win is 10.  In other words, it won 10 more games than the Committee expected.  Its teams played a total of 215 games.  So its winning 10 more games than expected represents it performing better than the Committee expected in 4.7% of its games.

An important feature of this and all the other methods is that the net differences always represent games against teams from other regions.  This is because in games between two teams from the same region, if one unexpectedly wins a game then the other unexpectedly loses and the win and loss cancel each other out thus producing a net difference of 0 for that game.

The notable feature of this table is that the Middle, North, and West regions all have positive net differences.  The South region has a negative net difference.

Expected Games Method

Here, the results are similar, but not identical, to those for the Actual Games Played method.  Again, the Middle, North, and West region have positive net differences.  The South has a negative net difference.

Unseeded Opponents At Neutral Sites Method

The notable feature of this table is that the West region teams tend to prevail in these games, at the expense of teams from the Middle and North regions.

Conferences

Actual Games Played Method

In the table, I have arranged the conferences in order with those that have won the highest percentage of games, as compared to expected wins, at the top.

The table covers 12 years of games.  Some conferences show fewer than 12 games due to conference membership changes over the 2011 to 2023 time frame.  For the conferences that have few games, I tend to not take the numbers very seriously -- the data sample is very small.  Taking that into consideration, here is what I see in the numbers from the other conferences:

• Tournament teams from some of the mid-majors tend to do better than the Committee expects.

• From the Power 5 conferences, the Big 10 does better than the Committee expects and the ACC does just as the Committee expects.  The Pac 12 does a little more poorly than the Committee expects.  The SEC and especially the Big 12 do more poorly than the Committee expects.

Expected Games Method

The table shows that the Big 10 does better than the Committee expects, followed by the Big West, West Coast, and Colonial conferences.  At the other end of the spectrum, the Pac 12 and Big 12 do considerably more poorly than the Committee expects, followed by the SEC and ACC.

An interesting aspect of this table, in relation to the bracketing rules, is the relationship among the Big West and West Coast conferences on the one hand and the Pac 12 conference on the other.  To a good extent, the Big West and West Coast teams' performing better than the Committee expects is at the expense of the Pac 12 conference, since the Big West and West Coast conference teams are the ones the Pac 12 teams tend to play in the early rounds of the Tournament, due to the NCAA's bracket formation rules (including the required use of the RPI and the travel expense limitation policy).

Another interesting aspect is that the Big 10 performs better than the Committee expects, but the other Power 5 conferences perform more poorly.

Unseeded Opponents At Neutral Sites Method

The notable feature from this table is that the Big West, West Coast, and Pac 12 conferences perform the best in these games.  They all are from the West region.  Teams from the other 4 Power 5 conferences perform at or close to a 50-50 ratio.  The West region conferences' good performance is balanced out by weak performance by teams from non-Power 5 conferences.

Summary and Comment

Looking at regions, teams from the South perform more poorly than the Committee expects.

Looking at conferences:

Although most of the ACC teams are in the South, its teams perform about as the Committee expects.  The SEC and Big 12, on the other hand, perform more poorly than the Committee expects.

From the West, the Big West and West Coast conferences perform better than the Committee expects, apparently at the expense of the Pac 12.  This suggests an unusually high degree of parity in the West.  Coupled with the other numbers above, it appears that the NCAA bracketing rules do not do well when there is a high degree of parity in a region.

From the Middle, teams from the Big 10 perform better than the Committee expects.

Comment:  Altogether, the numbers suggest that the NCAA bracketing rules result in there not being equal treatment among the regions and among some of the stronger conferences.  The Committee could improve on this by tracking "longitudinal" data and results such as I have done here and taking the data and results into consideration during the bracketing process.