SO YOUR CONFERENCE WANTS MORE OF ITS TEAMS IN THE NCAA TOURNAMENT: AS A GROUP, HOW MUCH ATTENTION SHOULD ITS TEAMS PAY TO THE RPI FORMULA? ANSWER: A LOT

"What is the best way to improve a team or conference RPI?  The simple, but correct answer to this common question is schedule and beat non-conference teams ranked higher in the RPI."

Jim Wright, NCAA Director of Statistics

Rick Campbell NCAA Assistant Director of Statistics

In March 2008, the NCAA's Frequently-Asked Questions About the Women's Soccer Rating Percentage Index included the above question and answer.  When I look at how teams do their non-conference scheduling today, it seems like this is the advice many follow.  But there's a problem:  For an individual team scheduling in isolation, the advice seems good.  But for a conference whose teams are scheduling as a group, the advice is wrong.  This article will explain why.

In my previous two articles, I showed that if a team has NCAA Tournament aspirations, it's very important that the team pay attention to the RPI formula when doing its non-conference scheduling.

In this article, I'll show that if a currently second tier conference aspires to have more than one team in the NCAA Tournament, it's very important that the conference teams as a group pay attention to the RPI formula when doing their non-conference scheduling.  By "second tier" I mean the top non-Power 5 conferences such as the Big East, American, Ivy, West Coast, Big West, Conference USA, and Colonial conferences.

I'll start with some points about the RPI formula and go from there to some tests I've done.

The RPI Formula.

Element 1.  Element 1 of the RPI formula is a team's winning percentage.  The effective weight of Element 1, in relation to a team's ultimate ratings, is 50%.  So, teams' winning percentages are very important.

From a conference perspective, winning percentage breaks into two sets of games: conference games and non-conference games.  For conference games, a conference's overall winning percentage always is 0.500 -- for every conference team win there is a matching conference team loss and for every tie by one conference team there is a matching tie by another conference team.  Although this seems elementary, it's important:  If conferences played only conference games, then so far as Element 1 is concerned, all the conferences would be equal since they all would have a winning percentage of 0.500.

Where the conferences distinguish themselves from each other, for Element 1, is in their non-conference games.  Looking at the 2018 season, here are the conferences' winning percentages in non-conference games, in order from best to worst:

As you can see, there is a clear separation of the "Power 5" conferences from the other conferences.  Why?  You might say, "Well, their teams, on average, are better."  Although that might (or might not) be true, it isn't the right answer.  The right answer is, "They scheduled smarter, in relation to Element 1, than the other conferences."

Take the Ivy, the American, the Big East, and the West Coast conferences, which are the next group in the table.  They could have scheduled non-conference opponents so as to have had better non-conference winning percentages, simply by scheduling weaker opponents than they actually scheduled.  They just didn't do it.  Put bluntly, they scheduled less smartly, in relation to Element 1, than the Power 5 conferences.

Element 2.  Element 2 of the RPI is the average of my opponents' winning percentages (against teams other than me -- which is an RPI detail you can ignore).  The effective weight of Element 2, in relation to a team's ultimate rating, is 40%.  So, my opponents' winning percentages also are very important.

Here again, I need to consider my conference opponents as one group and my non-conference opponents as another.

Suppose I'm a Big Twelve team.  Then looking at the above table, on average for each of my 9 conference games my Big Twelve opponent is going to contribute an 0.6944 winning percentage, merged together its conference winning percentage, to my Element 2.  On the other hand, suppose I'm a West Coast Conference team.  Then on average for each of my 9 conference games my opponent is going to contribute only 0.5550, merged together with its conference winning percentage, to my Element 2.  Simply put, my West Coast Conference compatriots didn't schedule as smartly, in relation to my Element 2, as my alter ego's Big Twelve conference compatriots.  And, let's be clear, those games' contributions to my Element 2 are going to be about half of all the Element 2 contributions I'll receive, so they matter a lot.

So, I want my fellow conference teams to schedule smartly, in relation to my Element 2.  Then I have to be willing to do the same for them.  In other words, I have to schedule so as to maximize my non-conference winning percentage.

If I want to schedule to maximize my non-conference winning percentage, then I need to identify a list of opponents I'm confident I can beat.  But, it doesn't end there.  I also want my non-conference opponents to make decent contributions to my Element 2.  As I showed in the preceding two articles, teams in the same ranking area can make quite different contributions to their opponents' Element 2s.  So, from my list of opponents I'm confident I can beat, I need to pick the ones that will make the best contributions to my Element 2 (rather than the ones that are the best ranked).  I then will have (1) helped my conference compatriots by maximizing my non-conference winning percentage and (2) helped myself by playing opponents from my list that are the best contributors to my own Element 2.

Element 3.  Element 3 of the RPI is the average of my opponents' opponents' winning percentages.  The effective weight of Element 3, in relation to a team's ultimate rating, is 10%.  So, Element 3 matters some, but not a lot.

There is one feature of Element 3, however, that is good to consider.  If I'm Texas, and I play Oklahoma, then all of Oklahoma's opponents contribute to my Element 3.  And, Oklahoma's opponents include all of my other Big Twelve compatriots.  So, just as I want my Big Twelve compatriots to make good contributions to my Element 2 when I play them, I want them to make good contributions to my Element 3 via their games with the other Big Twelve teams that I will play.

The Tests.

OK, so what I've said above is that, from an RPI perspective, I want all the teams in my conference to schedule so that they're highly likely to win each of their non-conference games.  And, for their non-conference opponents, from the list of teams they're highly likely to beat, I want them to pick the teams that will make the best contributions to their Elements 2.

It sounds good to me in theory, but would this scheduling system really work?  I conducted two tests, with the Big East as my guinea pig conference.  The tests show that it would improve the Big East teams' RPI rankings.  In fact, the amount of improvement is stunning.

Test 1

I used the entire Division I 2018 games and results data base for the test, with one exception.  The exception is that I changed the opponents for all of the Big East teams.  Here's how I changed them:

1.  For each team, I started with its actual 2018 ARPI rating.  I know from studies I've done that if my team's ARPI rating is roughly 0.0604 better than my opponent's rating (with the ratings adjusted for home field advantage), then my team will win roughly 75% of the time and as the rating difference increases, my winning percentage will increase.  So, I subtracted 0.0604 from each team's ARPI rating and identified the pool of all teams with ratings poorer than that number as the team's potential non-conference opponents.  I did this to assure that each team's chance of winning each non-conference game would be 75% or better.

2.  Thinking of myself as the scheduler, I then went through a process for my team, to see which teams from my pool would be the best to play from an RPI strength of schedule contribution perspective.  I know the rankings of all teams as contributors to their opponents' strengths of schedule, so for my team's pool of potential opponents I put the teams in order from the best strength of schedule contributor to the worst.  Big East teams ordinarily play 9 non-conference games, so ideally I would pick the 9 best strength of schedule contributors as my team's non-conference opponents.  I wanted the test to be realistic, however, and simply picking the 9 best contributors wouldn't have been geographically realistic, so instead of the 9 best contributors I picked the 9 best that looked geographically reasonable.  I did this for each  Big East team.  It was easier for some teams than others, due to their geographic locations.  At the end of this step, I had a full set of 9 non-conference opponents for each team.

3.  With my list of 9 non-conference opponents for each Big East team, I then compared each Big East team's ARPI rating to each of its opponents' ratings to determine the Big East teams' likelihood of winning each non-conference games.  Remember, for the opponents I selected, the win likelihood always is 75% or better.  With these likelihoods I then determined the average Big East win/loss/tie likelihood for all 90 of the non-conference games.  The result was that I could expect that each team, from its non-conference schedule, would win 80%, lose 10%, and tie 10%.  This, of course, didn't fit well with 9 non-conference games, so I decided to be conservative:  I would set the game results so that each Big East team won 7 of its non-conference games, lost 1, and tied 1.

4.  With each team's non-conference opponents and game results in hand, I then deleted all of the teams' actual 2018 non-conference games from the 2018 schedule and replaced them with my test non-conference games and results.

5.  Now came the fun part:  I gave Excel a Calculate command.

With these Big East schedule changes, here are the top nine conferences' winning percentages in non-conference games, in order from best to worst:

The Big East now has the best conference winning percentage.  So, what does this do for its teams' rankings?

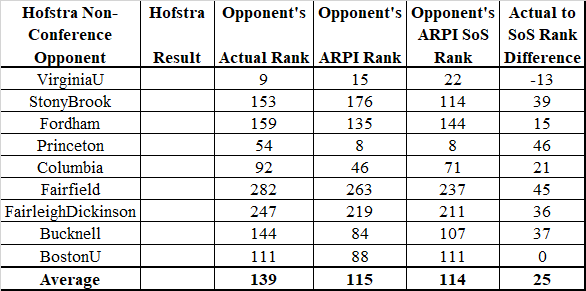
For the actual 2018 season, here is what the Big East teams' ARPI rankings and their rankings as strength of schedule contributors were:

With their substituted schedules, here are what the teams' numbers would be:

As I said, the results of this changed approach to non-conference scheduling are stunning.  The Big East's average ARPI rank jumped 45 positions and its average rank as a strength of schedule contributor jumped 73 positions.  It went from three Top 60 teams to seven.  It went from one sure bet team for an NCAA Tournament berth plus two bubble teams to a likely six in the Tournament plus one bubble team.

Test 2 Method

Test 1 is a "looking backwards and asking 'What if we had done this?'" kind of test.  Test 2 is a "looking forward and asking 'What if we do this?'" test.

In this test, I went through the same process as I did for Clemson as described in the article "So You Want an At Large Position in the NCAA Tournament:  How Much Attention Should You Pay to the RPI Formula, In Your Non-Conference Scheduling?  Answer: A Lot," which is two articles above this one.  I won't repeat the explanation of the method here, other than to say:

• It uses the 2018 games data base (but not the 2018 results).
• It uses my assigned 2019 simulated ratings to determine game outcomes.
• I replaced all of the Big East non-conference opponents with the same opponents I used in Test 1.

The way this test works, the system treats all games where the location-adjusted rating difference between teams is less than 0.0150 as ties.  It treats all other games as wins by the better rated team.  It then applies the ARPI formula to all of the game results.

Here are the Big East team's ARPI rankings under this test:

These results are in the same ball park as in Test 1, but show the Big East's average ARPI rank as 10 positions better than in Test 1.

Conclusion.

If a conference's teams, as a group, are determined to maximize their ARPI ranks, then they need to base their non-conference scheduling on how the RPI formula works.  Each conference team would schedule opponents it is highly likely to beat and, of potential opponents that meet that criterion, they would pick those opponents likely to be the best strength of schedule contributors under the RPI formula.

As probably is obvious, this means the conference would schedule non-conference opponents in a way that is very different than what it's done in the past.  Whether a conference would want to do this, once it sees what it's list of non-conference opponents looks like, is something I can't answer.  There might be criticisms that it "isn't right" for a conference's teams to systematically schedule only non-conference opponents they can beat.

On the other hand, if the name of the game is getting your conference's teams into the NCAA Tournament, the NCAA, in adopting the RPI as the rating system the Women's Soccer Committee must use, has defined the rules of the game.  Those rules say this is how you should schedule.  If critics don't like it, the correct response is to change the rules of the game, which would mean replacing the RPI with something better.

PAYING ATTENTION TO THE RPI FORMULA IN YOUR NON-CONFERENCE SCHEDULING: FOLLOW UP

I my previous post I described an experiment I ran to see how much non-conference scheduling matters.  The experiment's results said that it matters a lot -- indeed, a whole lot.  In fact, it mattered so much that wanted to come up with a new and different experiment to see if it would produce similar results.

In the new experiment, I started with the 2018 season exactly as played.  That season ended up with Clemson having an ARPI rank of #46 (although Massey gave them a rank of #22).  In that season, here are Clemson's opponents with the game locations and results, plus the opponents' ARPI ranks, ranks as contributors to opponents' strengths of schedule, and Massey ranks (which I consider to be the best indicators of the opponents' true strength):

What's most notable here is that Clemson's opponents' average rank as contributors' to its strength of schedule was considerably poorer than their average ARPI rank and even more poor than their average Massey rank.

For the experiment, I simply substituted, for each opponent, a different opponent with a better rank as contributor to opponents' strengths of schedule:

As you can see, the opponents' average ARPI ranks are the same as they were for Clemson's actual schedule.  In other words, from an RPI formula perspective, the two schedules were equal in strength.  But look at the opponents' average rank as contributors to Clemson's strength of schedule.  They now are much better than the opponents' average ARPI rank.  And, they are 91 rank positions better than under the schedule Clemson actually played.  Plus, according to Massey, this experiment schedule actually is significantly weaker than the ARPI says it is and much weaker than Clemson's actual schedule was.

So, as stated above, according to the ARPI formula, based on Clemson's actual schedule, their rank was #46.  With the substitute opponents, but same results, what does the ARPI formula say its rank is?  #23!  Even though playing an equally difficult schedule according to the ARPI and a significantly easier schedule according to Massey.

But, according to Massey, when I substituted Radford for Oregon as an opponent, I substituted a #108 team for a #56 team.  Clemson lost to Oregon, so in alternative schedule experiment I have Clemson losing to Radford.  Suppose Massey is right and Radford is much weaker than Oregon.  Then it's fair to expect that Clemson would beat Radford.  If I change the experiment to give Clemson a win in that game, the ARPI formula now gives it a rank of #17.

And further, when I substituted South Florida for South Carolina, according to Massey I substituted a #30 team for a #18 team.  Suppose Massey is right about South Florida.  If I change the experiment to give Clemson a win in that game, the ARPI formula now gives it a rank of #8.

The point of all this is:  Clemson, by playing a 2018 schedule intended to maximize its ARPI rank, could have ended up with a rank in the #8 to #23 area, rather than the #46 it actually received.  And it could have done this with a schedule that would look equally as strong as the one it actually played, so far as the Women's Soccer Committee would be concerned.

Conclusion.  My first experiment said that if you schedule with a view to how your schedule will relate to the RPI formula, it can make a whole lot of difference in what your final ARPI rank will be.  It made so much of a difference that I wanted to do a different experiment to see if it produced relatively similar results.  I did perform that experiment, as described above, and it confirmed what the first experiment indicated.  If you schedule with a view to how your schedule will relate to the RPI formula, it can make a whole lot of difference for your final ARPI rank.

SO YOU WANT AN AT LARGE POSITION IN THE NCAA TOURNAMENT: HOW MUCH ATTENTION SHOULD YOU PAY TO THE RPI FORMULA, IN YOUR NON-CONFERENCE SCHEDULING? ANSWER: A LOT.

A funny think happened on the way to ... updating a scheduling tool.  (The tool lets a team see how potential non-conference opponents might affect its RPI rating and NCAA Tournament prospects.)  I saw that I could do an experiment to show how important it is to schedule your non-conference opponents with a view to how the RPI works.  So, I ran the experiment.  The results are startling, even to me.

Here's a brief description of the experiment:

First, I reviewed each team's rating history and from that, using statistical tools, assigned each team a rating.  In the experiment, each team's assigned rating and rank is its actual strength.  Each team always performs at this actual strength level.

Second, I took last year's regular season schedule and determined the outcome of every game, based on the teams' actual strength and the value of home field advantage.  Based on in-conference results, I also set up conference tournaments including their outcomes based on the teams' actual strength and the value of home field advantage.

Third, with all those game results as the data base, I applied the NCAA's ARPI formula to see what ratings and ranks the formula would give to teams.

So, you'd expect that teams' ranks at the end of the process using the NCAA's ARPI formula would be about the same as the actual strength ranks I assigned them and that determined the outcomes of all games, right?

Not exactly.  In fact, in many cases teams' ranks according to the NCAA's ARPI formula are not close to their actual strength ranks.  And this includes a significant number of cases in which it would matter for NCAA Tournament at large selection purposes.

Here's a table that demonstrates that, with an explanation below the table:

In the table, the Simulated 2019 Rank column is the actual strength ranks I assigned, for the top 125 the teams.  In the experiment, these are the ranks that determined the outcomes of all games.  The 2019 ARPI Rank column is the ranks the NCAA's ARPI formula gave the teams after applying the formula to the game results that the actual strength ranks produced.  In each rank column, I've color coded the top 60 teams.  In the column with the team names, I've color coded blue the teams that are within the actual ranks top 60 but outside the ARPI formula's top 60.  I've color coded grey the teams that are outside the actual ranks top 60 but within the ARPI formula's top 60.  I've focused on the top 60 because, for practical purposes the ARPI formula's top 60 are the teams the Women's Soccer Committee considers as potential candidates for at large selections.  (In fact, no team ranked poorer than #57 has gotten an at large selection over the last 12 years.)

As you can see, there are 13 teams whose actual strength puts them in the top 60, but that are outside the ARPI formula's top 60.  And conversely, there are 13 teams whose actual strength puts them outside the top 60, but that are inside the ARPI formula's top 60.

So, why are there differences between teams' actual strength ranks and the ranks the ARPI formula gives them?  The differences are due to one, and only one, thing:  the interaction between the NCAA's RPI formula and the teams' schedules.

I'm going to use Clemson's and Hofstra's results, in my experiment, to show this.

CLEMSON

In the experiment, Clemson's actual strength rank is #20, and all its results are consistent with that rank.  Yet the NCAA's RPI formula, when applied to those results, comes up with a rank of #74.  How can that be?

It is because of the way the NCAA's RPI measures strength of schedule.  An opponent contributes to Clemson's strength of schedule based on the opponent's own winning percentage (against all the teams it played other than Clemson) and on its opponents' opponents' winning percentages.  Under the RPI formula the effective weights of these two elements are roughly 80% the opponent's own winning percentage and 20% the opponents' opponents' winning percentages.  In other words, the opponent's winning percentage is by far the strongest factor in the strength of schedule part of the RPI formula.  Since most of what a team contributes to your strength of schedule is its winning percentage, this means that if you are looking at two teams with similar rankings, where one of them will fill a possible opponent slot in your schedule, you will be better off from an RPI formula perspective playing the team that will have the better winning percentage.

Here is a table for the in-conference ACC opponents Clemson played in my experiment (the ones it actually played in 2018):

In this table, teams' Actual Ranks are the actual strength ranks I assigned them, which determined the results of all games.  The ARPI Ranks are the teams' ranks as determined by the NCAA's ARPI formula, applied to those game results.  As you can see, in some cases the ARPI formula has seriously mis-ranked teams.  The ARPI SoS Rank is the ARPI formula's rank of each opponent as a contributor to its opponents' strengths of schedule.  As you can see, here again the ARPI formula has seriously mis-ranked teams.  The Actual Rank to SoS Rank Difference is the difference between a team's actual strength rank and the rank the ARPI formula has assigned it as a contributor to its opponents' strengths of schedule.

At the bottom of the table are averages.  Looking at that row, the average actual rank of Clemson's in-conference ACC opponents was 61.  On the other hand, the ARPI formula only gave them an average rank of 73, meaning it under-ranked them by an average of 12 positions.  And, as contributors to Clemson's strength of schedule, the ARPI formula only gave them an average rank of 115, meaning it under-ranked them by an average of 54 positions.

There's nothing Clemson can do about who its in-conference ACC opponents are.  It's simply a fact of Clemson's life that the ARPI under-ranks them and that it under-ranks them even more as contributors to Clemson's strength of schedule.

So what does the table look like for Clemson's non-conference opponents?  Here it is:

As you can see, the average actual strength rank of Clemson's non-conference opponents is 122.  But the ARPI formula calculates their average rank as only 153, 31 positions poorer.  And, their average contribution to Clemson's strength of schedule is only 184, 62 positions poorer.

When you put together the ARPI formula's under-ranking of Clemson's in-conference ACC opponents as strength of schedule contributors with the formula's similar under-ranking of Clemson's non-conference opponents, you get Clemson, with an actual strength rank of #20, receiving an ARPI formula rank of #74.  At #20, Clemson would be a sure thing for an at large selection for the NCAA Tournament.  At #74, it's out of the running.

So, could Clemson balance out its in-conference problem with better non-conference scheduling?  Yes.  Here's an alternative non-conference schedule that is equal in actual strength:

Where does this alternative schedule put Clemson?  At #23 in the ARPI formula's rankings, 51 positions better than the actual schedule put it and right about where it should be given its actual strength rank of 20.  And this is notwithstanding that the actual schedule and the alternative schedule have opponents essentially equal in actual strength.  Simply put, smart scheduling in relation to the RPI formula has balanced out the problem Clemson has due to its ACC opponents' contributions to its strength of schedule being understated.

What's more, the Women's Soccer Committee if looking at the alternative schedule will think that Clemson has played non-conference opponents with an average rank of 99, since that is their average rank under the RPI formula.  This is as compared to an average rank of 153 that the Committee will be seeing if looking at the actual schedule.

In other words, if you're Clemson in this experiment, smart scheduling in relation to the RPI formula is essential to realizing your NCAA Tournament aspirations.  With Clemson's actual 2018 schedule, it's not in the Tournament.  With an RPI-smart schedule, it's in.

But, there's one more bonus from Clemson's alternative "smart" schedule.  Here's what its in-conference ACC table will look like when paired with that schedule:

This table shows that if Clemson plays the alternative "smart" schedule, its in-conference ACC opponents' average ARPI rank is 71.  This is 2 positions better than if Clemson plays the actual schedule.  In shifting schedules, Clemson hasn't changed its own winning percentage, but it has played opponents with better winning percentages.  This, in turn, gets passed on to Clemson's ACC opponents through Clemson's contribution to their strengths of schedule.

Thus Clemson's smart scheduling can give it a large ARPI benefit and, at the same time, also can give a small benefit to its ACC opponents.

HOFSTRA

With Hofstra, for illustration, I'm going to show how poor scheduling can take a team from a good rank to a poor one.

In the experiment, Hofstra's actual strength rank is 70.  But, with its actual schedule, the ARPI formula gives it a rank of 28.  Let's look at its tables to see how this happened.

Here's its in-conference Colonial actual schedule:

You can see from this table that the ARPI formula, on average, under-ranks Colonial teams as contributors to their opponents' strengths of schedule, by 23 positions.  This is similar to what the formula does to ACC teams except that for the ACC the problem is much more severe.

Here's Hofstra's actual non-conference schedule:

What you can see here is that (1) the RPI formula gives Hofstra's non-conference opponents significantly better ranks than their actual strength ranks and (2) the RPI formula likewise gives the non-conference opponents significantly better ranks as strength of schedule contributors.  The result of this is that Hofstra, with an actual strength rank of 70 gets an RPI formula rank of 28.  (This isn't just due to Hofstra's non-conference scheduling.  Its smart scheduling is moving it up in the rankings, and other teams' not-smart scheduling is moving them down in the rankings.  The cumulative effect of this is Hofstra ending up at #28.)

Suppose Hofstra had scheduled differently.  Here's an alternative non-conference schedule of equal actual strength but producing competely different ARPI formula results:

With this non-conference schedule, Hofstra drops from the ARPI formula's rank of 28 to the formula's rank of 63.  Yet this alternative schedule is equal in actual strength to Hofstra's actual schedule.  It's just that these teams, due to the structure of the RPI formula, result in the formula grossly under-stating Hofstra's strength of schedule.

SUMMARY

If you're a team with NCAA Tournament aspirations, it's critical to schedule non-conference opponents with a view to how the RPI formula will see them as strength of schedule contributors.  Especially if you're in a strong conference where it's hard to have a really good winning percentage, you're going to need all the boost to your strength of schedule that you can get.  And, teams roughly equal in actual strength and in RPI rank often are not equal in strength of schedule contributor rank.  So in selecting opponents, it's critical to pick ones not only who meet your objectives in terms of their actual strength and RPI rank, but also who will make good contributions to your RPI strength of schedule.

If you want a good tool for evaluating potential opponents with a view to their histories of actual strength, ARPI ranks, and ranks as contributors to opponents' strengths of schedule, there's a tool I created that's available at the RPI for Division I Women's Soccer website.  It's in the form of a downloadable Excel workbook (free) and is an attachment at the bottom of the NCAA Tournament: Scheduling Towards the Tournament page.  It has a page for each team from which you can get a picture of whether the team would be a good one for you to play given your schedule objectives.  And it has summary pages that can be helpful.  And, on its first page, it has a User Manual.

Remember, scheduling with a view to how the RPI formula will interact with your schedule matters.  A lot.